我们的主角真是太帅了！

论文答辩、送审等七七八八的事情终于结束了，相关评审也告一段落。感谢王宝土老师和学校电脑店的大力相助，毕设《寻星之路》demo终于是有惊无险地完成了它的使命。说实话我对这个作品可能不是太满意，因为它比我最开始设想的“三个章节、25个关卡、精妙绝伦的故事”相差甚远，仅两个月的独立开发时间，构思就浪费了小半个月，可叹。

在毕业答辩的技术部分中，占比相当大的就是接下来要介绍的 A* 了（另一部分是行为树，可以看看我的上一篇文章）。作为毕设的复盘，我将在这篇文章里聊聊我是怎么实现A*的，以及A*可以有哪方面的一些优化。

什么是A*？

A*是一种启发式搜索算法，是一种在平面上有多个节点的路径，求出最低通过成本的算法。该算法综合了最良优先搜索和 Dijkstra 算法的优点：在进行启发式搜索提高算法效率的同时，可以保证找到一条最优路径。

Dijkstra算法
Dijkstra算法使用类似广度优先搜索的方法解决赋权图（只能用在权重为正的图中）中的单源最短路径问题，其思想如下：

从源节点（起点）出发，寻找它与图中所有其它节点之间的最短路径。
记录当前已知的最短路径，并在寻找到更短的路径时更新。
一旦找到源节点与其他节点之间的最短路径，那个节点会被标记为“已访问”并添加到路径中。
重复寻找过程，直到图中所有节点都已经添加到路径中。这样，就可以得到从源节点出发访问所有其他节点的最短路径方案。

Dijkstra 对于查找起点到任意点的最短路径很有用，但对于点到点的路径查找就很浪费了。

之所以说A*是启发式的，是因为它基于启发式函数和节点优先级的。这里有一个用于确定节点优先级的公式：

f(n) = g(n) + h(n)

其中,

$g(n)$ 是节点 n 距离起点的代价。
$h(n)$ 是节点 n 距离终点的预计代价，这也就是A*算法的启发函数。
$f(n)$ 是节点 n 的综合优先级。当我们选择下一个要遍历的节点时，我们总会选取综合优先级最高（ $f(n)$ 值最小）的节点。

如果有多个节点的 $f(n)$ 相同该怎么办？它们可能都会被搜索，尽管我们只需要搜索其中的一条路径。为了解决这个问题，我们可以考虑在 $f(n)$ 相同时选择 $h(n)$ 最小的节点进行搜索。

当 $h(n)$ 也相同时，可以为启发函数添加一个附加值（附加值对于结点必须是确定性的，不能是随机的），而且它必须让 $f(n)$ 体现区别，即 $h(n)$ *= (1 + p)。选择因子 p 使得 p < 移动一步的最小代价 / 期望的最长路径长度。假设你不希望你的路径超过1000步（step），你可以使p = 1 / 1000。添加这个附加值的结果是，A*比以前搜索的结点更少了.

启发式函数 $h(n)$

f(n) = g(n) + h(n)

启发式函数可以控制A*的行为，控制算法的速度和精确度。在一些情况下，我们可能未必需要最短路径，而是希望能够尽快找到一个路径即可，这也是A*算法比较灵活的地方：

一种极端情况，如果 $h(n)$ 很小或者是0，则只有 $g(n)$ 起作用，此时A*演变成 Dijkstra 算法，这保证能找到最短路径
如果 $h(n)$ 经常都比从 n 移动到目标的实际代价小（或者相等），则A*保证能找到一条最短路径。 $h(n)$ 越小，A*扩展的结点越多，运行就得越慢
如果 $h(n)$ 精确地等于从 n 移动到目标的代价，则A*将会仅仅寻找最佳路径而不扩展别的任何结点，这会运行得非常快。尽管这不可能在所有情况下发生，你仍可以在一些特殊情况下让它们精确地相等
如果 $h(n)$ 有时比从 n 移动到目标的实际代价高，则A*不能保证找到一条最短路径，但它运行得更快
另一种极端情况，如果 $h(n)$ 比 $g(n)$ 大很多，则只有 $h(n)$ 起作用，A*演变成 BFS 算法

那么我们应该怎么定义 $h(n)$ 呢？在《寻星之路》中，我使用的是二维网格地图，而对于网格形式的图有以下这些启发函数可以使用：

如果图形中只允许朝上下左右四个方向移动，则可以使用曼哈顿距离（Manhattan distance）。
如果图形中允许朝八个方向移动，则可以使用对角距离。
如果图形中允许朝任何方向移动，则可以使用欧几里得距离（Euclidean distance）。

曼哈顿距离

如果图形中只允许朝上下左右四个方向移动，则启发函数可以使用曼哈顿距离，它的计算方法如下图所示：

public int CalDis(Vector2 start, Vector2 end, int d) {
    int dx = Math.abs(start.x - end.x);
    int dy = Math.abs(start.y - end.y);
    // d是两个相邻节点之间的移动代价，通常是一个固定的常数。
    return d * (dx + dy);
}

对角距离

如果图形中允许斜着朝邻近的节点移动，则启发函数可以使用对角距离。它的计算方法如下：

public int CalDis(Vector2 start, Vector2 end, int d, int d2) {
    int dx = Math.abs(start.x - end.x);
    int dy = Math.abs(start.y - end.y);
    // d是两个相邻节点之间的移动代价，d2指的是两个斜角节点之间的移动代价，对于正方形格子来说是根号二d
    return d * (dx + dy) + (d2 - 2 * d) * Math.min(dx, dy);
}

欧几里得距离

如果图形中允许朝任意方向移动，则可以使用欧几里得距离。欧几里得距离是指两个节点之间的直线距离，因此其计算方法也是我们比较熟悉的：

\sqrt{(p2.x - p1.x)^{2} + (p2.y - p1.y)^{2}}

其函数表示如下：

public int CalDis(Vector2 start, Vector2 end, int d, int d2) {
    int dx = Math.abs(start.x - end.x);
    int dy = Math.abs(start.y - end.y);
    // d是两个相邻节点之间的移动代价，d2指的是两个斜角节点之间的移动代价，对于正方形格子来说是根号二d
    return Math.sqrt(dx * dx + dy * dy);
}

实现

A*的具体实现依靠两个列表：开启列表和关闭列表。步骤如下：

把起点加入开启列表（按该点到E点的距离排序+走过的步数从小到大排序）
如果开启列表不为空，则从开启列表中选取优先级最高的节点n：
1. 如果节点 n 为终点，则：
  - 从终点开始逐步追踪 parent 节点，一直达到起点；
  - 返回找到的结果路径，算法结束；
2. 如果节点 n 不是终点，则：
  - 将节点 n 从开启列表中删除，并加入关闭列表中；
  - 遍历节点 n 所有的邻近节点：
    - 如果邻近节点 m 在关闭列表中，则跳过
    - 如果邻近节点 m 不在开启列表中，则：
      - 设置节点 m 的 parent 为节点 n
      - 计算节点 m 的优先级
      - 将节点 m 加入开启列表中
反复执行第二步直到终点被添加进关闭列表（找到路径）或开启列表为空（无法到达）。

A*优化

优先队列（堆）

我们每次都需要从开启列表中找到 $f(n)$ 最小的节点，如果用列表存储节点的话，难免会在每次检索时都遍历一次列表，造成性能上的开销。我们可以考虑用优先队列（小顶堆）实现开启列表，这样每次开启队列的顶端都是 $f(n)$ 最小的节点。

通过优先队列，往开启队列中添加、删除的时间复杂度均为 $O(\log{n})$ 。

另外，开启列表选择的排序算法的稳定与否会影响寻路的结果，因为存在多个节点的 $f(n)$ 相同的情况。如果排序是稳定的，那么每次得到的路径都相同。

获取邻居的方式

这个问题可能是很多人没有考虑到的，那就是我们在获取一个节点 n 的所有邻居节点 m 时，可能是按照某个固定顺序（例如上下左右）遍历的。在这个顺序下，A*就会优先向上试探邻居节点，这无意中导致“向上走”这一策略变成了优先级最高的策略，接着才是向下、向左、向右。

为了打散固定的遍历模式，得到更多潜在的路径，我们可以在获取邻居这一步操作时添加获得某种排序方式的概率，例如上下左右、上左下右、右上左下几种顺序的概率各不相同。

JPS（跳点搜索）

JPS 是 A* 在邻居搜索这一步操作上的优化，但它只允许使用在能走斜线的情况下。JPS的寻路速度比A*快非常多，因为JPS减少了邻居的数量，不需要像A*一样搜索所有邻居，而是去搜索跳点，对跳点进行择优选择。要了解JPS，我们需要先理解几个概念：

强迫邻居
当节点 x 的八个节点中存在障碍，且节点 x 的父节点 p 经过节点 x 到达节点 n 的距离代价总是小于不经过节点 x 到达节点 n 的任意路径的距离代价，则称节点 n 为节点 x 的强迫邻居。
也就是说，节点 x 是最短路径的必经节点。

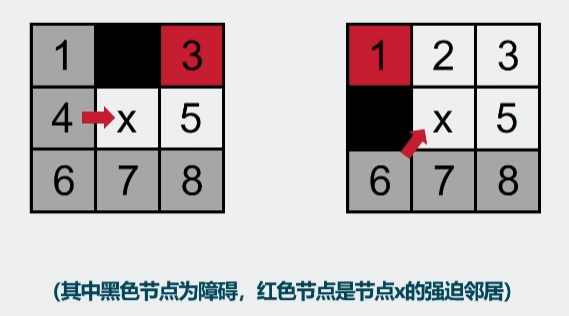
为什么上面右图中的节点 5 不是节点 x 的强迫邻居呢？这就涉及到了第二个概念：

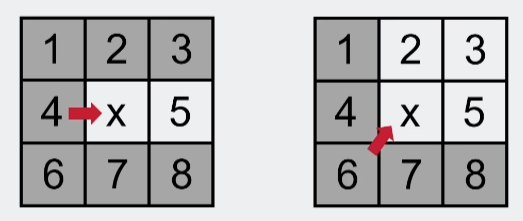
邻居裁剪
邻居裁剪的目的是避免相邻父子节点处理到共同邻居，从而不会产生多条等价的路径。
对于节点 x ，它的八个节点其实分为劣性节点和自然节点。
- 劣性邻居：从父节点 p 出发且不经过节点 x，所到达的节点的代价小于等于从父节点 p 出发经过节点 x 再到达该节点的代价
- 自然邻居：除了劣性邻居之外的节点（包括节点 x 本身）。
  强迫邻居必然由劣性邻居进化而来（不理解可以看看劣性邻居的定义），我们不需要考虑自然邻居，这一步就是邻居裁剪。
跳点
对于一个节点，只要它满足以下三条规则之一就可以被称之为“跳点”：

节点 x 是起点或终点
节点 x 至少有一个强迫邻居
节点 x 的父节点 p 在斜线方向，并且节点 x 的直线方向（水平或垂直）上存在满足条件一或条件二的节点

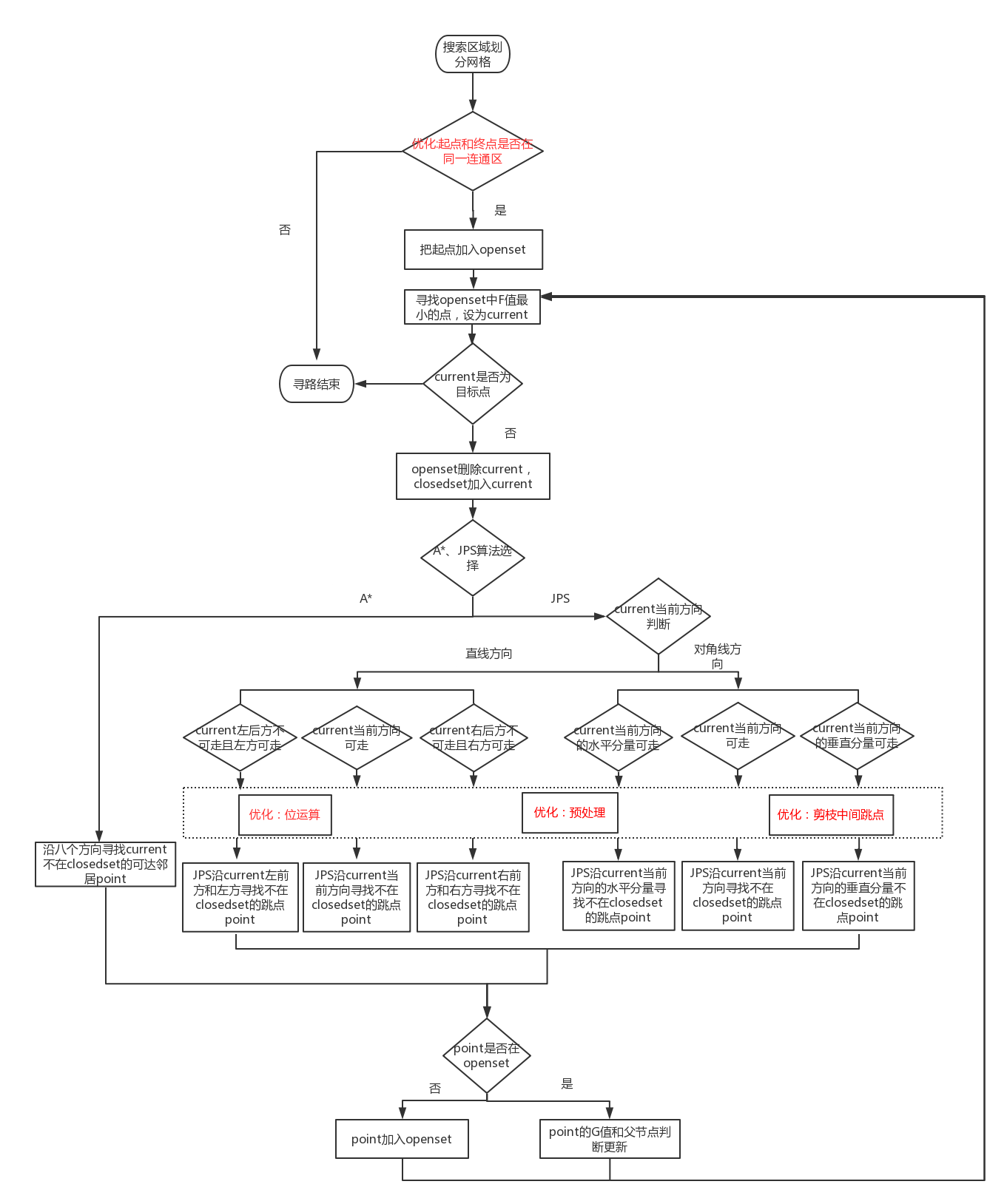
有了跳点，按照“先直线再斜线”的规则搜索跳点即可找到路径，具体流程如下：

若节点 x 当前搜索方向是直线方向：
- 如果current左后方不可走且左方可走（即左方是强迫邻居），则沿current左前方和左方寻找不在关闭列表的跳点；
- 如果current当前方向可走，则沿current当前方向寻找不在关闭列表的跳点；
- 如果current右后方不可走且右方可走（右方是强迫邻居），则沿current右前方和右方寻找不在关闭列表的跳点；
若current当前方向为对角线方向：
- 如果current当前方向的水平分量可走（例如current当前为东北方向，则水平分量为东，垂直分量为北），则沿current当前方向的水平分量寻找不在closedset的跳点；
- 如果current当前方向可走，则沿current当前方向寻找不在关闭列表的跳点；
- 如果current当前方向的垂直分量可走（例如current当前为东北方向，则水平分量为东，垂直分量为北），则沿current当前方向的垂直分量寻找不在关闭列表的跳点。
回溯所有跳点，我们就得到了一条路径

我们不难发现JPS主要的开销在“寻找跳点”上，需要遍历大量节点。但如果我们采用预处理提前找好地图中的所有跳点，这样就能避免浪费时间在搜索所有跳点上了，这样的JPS也被称为JPS+算法。这种以空间换时间的优化思路，速度最高可达A/*算法的273倍。

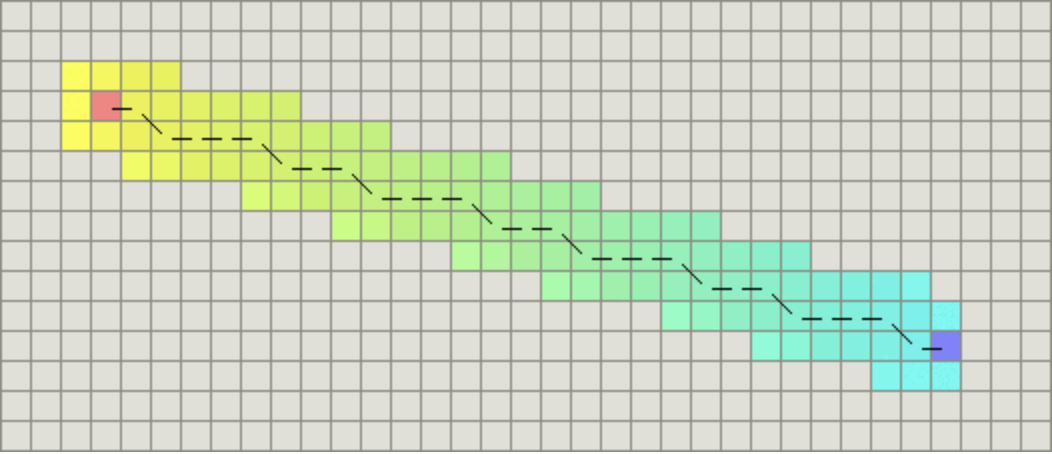
减少拐点

减少拐点是什么意思呢？就比如说下图中的两条路径，路径2（红色）的拐点数量为1，显著小于拐点数量为5的路径1（黑色）。

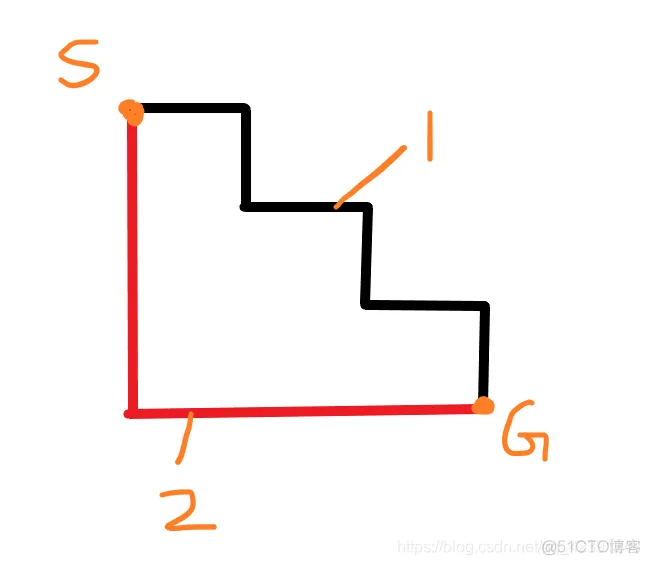
要达到这个效果，我们需要修改A*的启发函数：

f(n) = g(n) + h(n)

我们可以为其加上一个额外的权重 $C$ ，用来控制 $F(n)$ 的结果：

f(n) = g(n) + h(n) + C

当一个节点 x 为父节点 p 的拐点时，增大其 $C$ 值，降低拐点的权重。

超大地图？

可以采用JPS+算法或层次A*。JPS+前文已经介绍过了，我们来聊聊层次（分层）A*。在处理超大地图（例如一个10000 * 10000的二维地图）时，我们如果直接在起点和终点之间采用A*寻路，这个计算量是很可怕的，玩家需要等待一定时间才能得到算法返回的路径，无法保证超大地图下寻路的实时性。

分层A*的想法基于将大地图拆分成多个小的子地图区块，并预先计算出每个小地图区块与周围四个地图区块在边界上的互通点，然后在小地图区块内使用A*对找出的互通点做连通性测试并将结果保存下来，这就是预处理，有了这些“低级别的路径”，我们可以以更低的成本在更高级别上有效地进行寻路。预处理在小地图区块发送阻挡物变更时执行。

如果起点和终点相隔几个小地图，那么寻路流程如下：