基于快速傅里叶变换(FFT)的水体模拟

请注意
本文含有大量公式，涉及大量理论和计算，建议阅读时自行推导
可能有没写清楚的地方，这几天我修一下博客评论区

FFT全称为Fast Fourier Transform，即快速傅里叶变换，因其卓越的视觉模拟效果而被应用于好莱坞的影视行业中。经典电影《泰坦尼克号》中的海水就是由FFT实现的。这种模拟方法最早于2004年在Jerry Tessendorf的 Simulating Ocean Water 论文中提出。论文原文：https://people.cs.clemson.edu/~jtessen/reports/papers_files/coursenotes2004.pdf

快速傅里叶变换是快速计算序列的离散傅里叶变换（DFT）或其逆变换的方法。傅里叶分析将信号从原始域（通常是时间或空间）转换到频域的表示或者逆过来转换。FFT会通过把DFT矩阵分解为稀疏（大多为零）因子之积来快速计算此类变换。因此，它能够将计算DFT的复杂度从只用DFT定义计算需要的 $O(n^{2})$，降低到 $O(n\log n)$，其中 $\displaystyle n$ 为数据大小。
快速傅里叶变换广泛的应用于工程、科学和数学领域，它被IEEE科学与工程计算期刊列入20世纪十大算法。

前置知识

用FFT写海洋需要非常多前置知识，例如傅里叶级数、傅里叶变换、离散傅里叶变换、快速傅里叶变换，此外还需要扎实的微积分基础。

傅里叶级数

对任何一个周期性的信号，可以用一系列正弦函数相加的级数来拟合。信号与傅里叶级数的关系如下图所示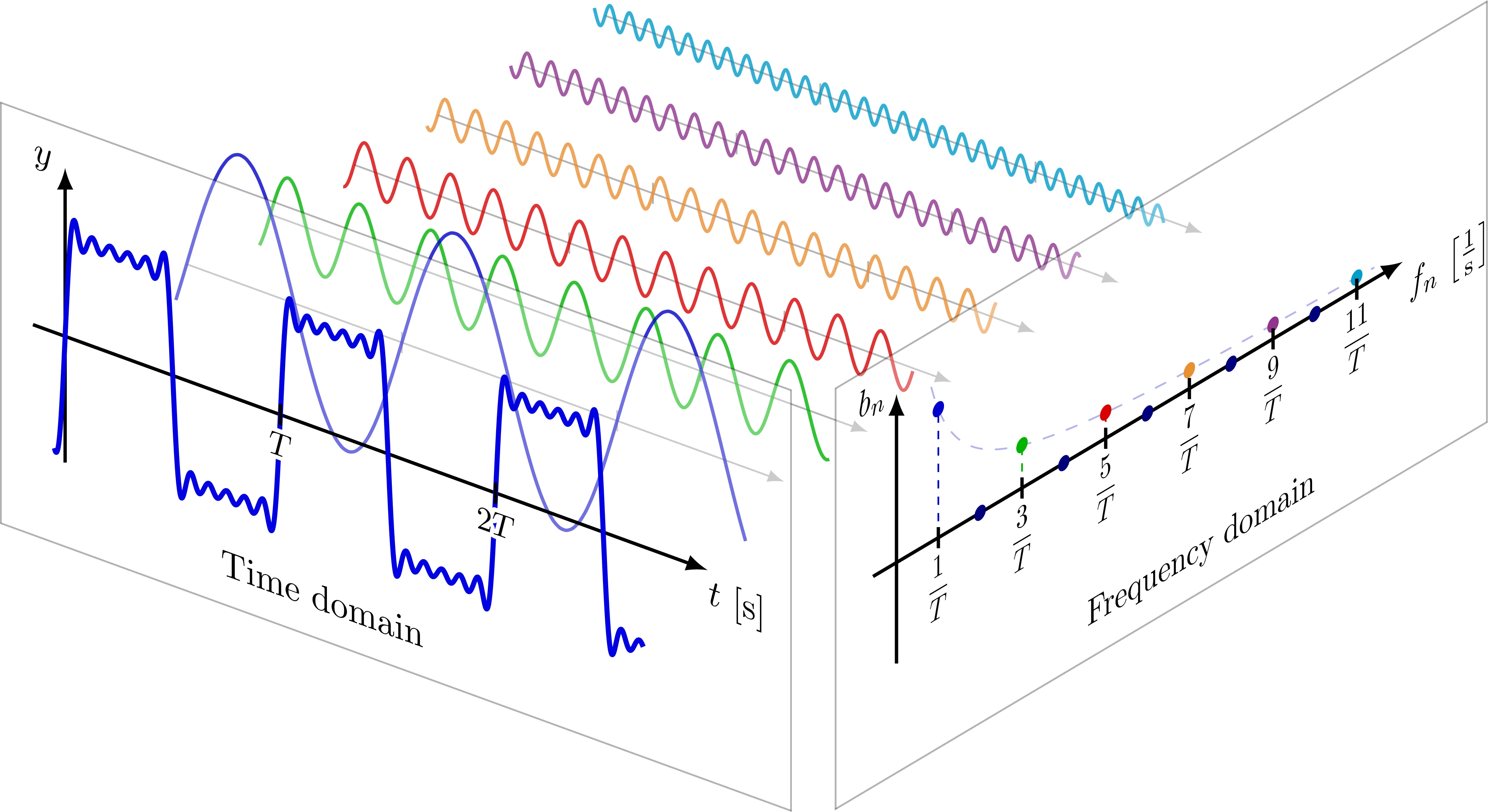

原始的信号图像称为**时域(Time Domain)，表示该信号随时间变化表现的周期形式。傅里叶级数部分则表示为频域(Frequency Domain)**，根据级数每一项的振幅A，可以绘制出对应的频域图。

傅里叶变换

现在我们有一个很漂亮的周期函数，它的频率是3Hz。如果我们定义一个二维笛卡尔坐标系来表示这个波（从原点指向曲线，长度与波对应点的纵坐标相同），可以得到不同旋转周期一系列图像。

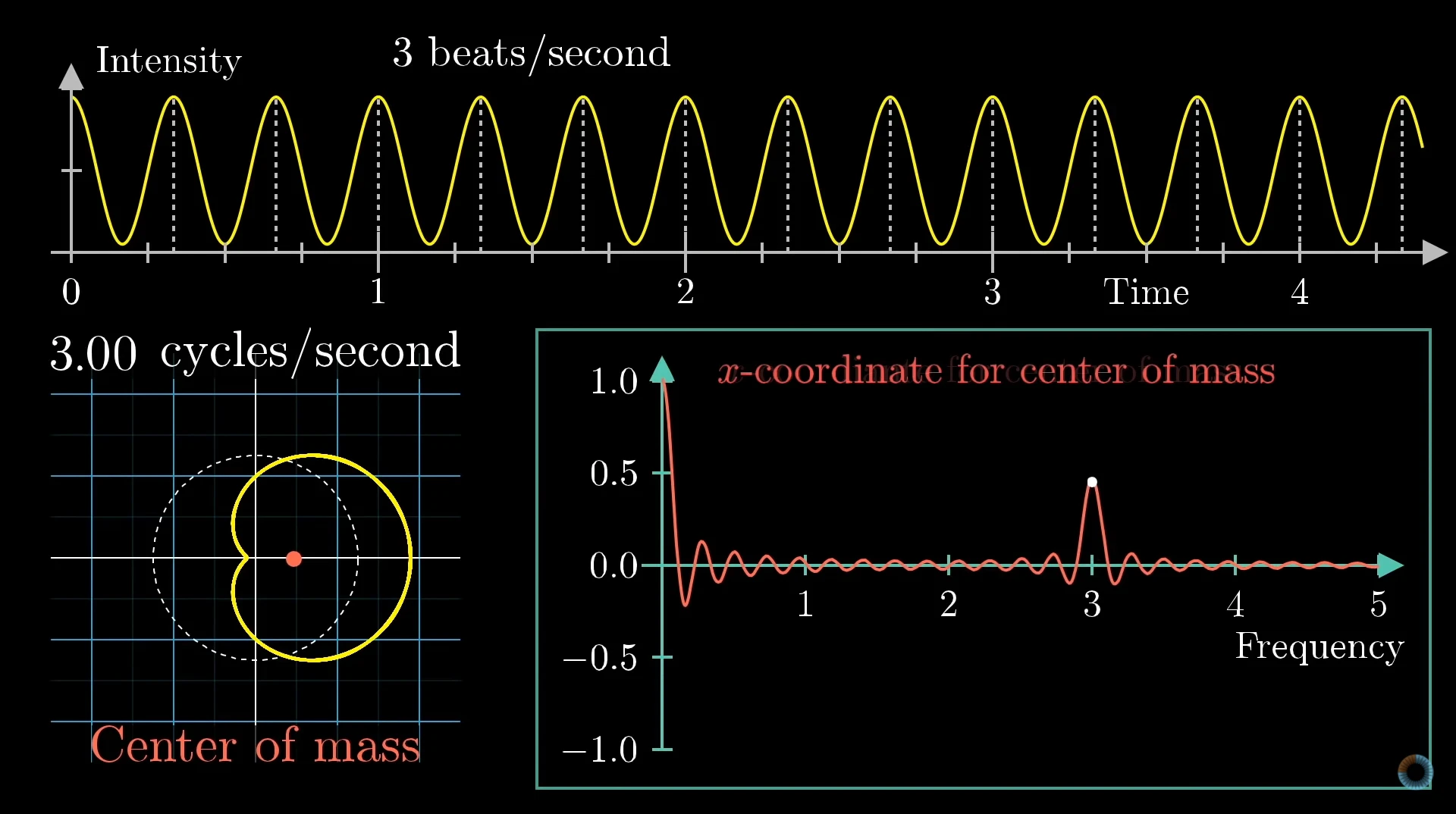
1/3 秒钟旋转 1 周
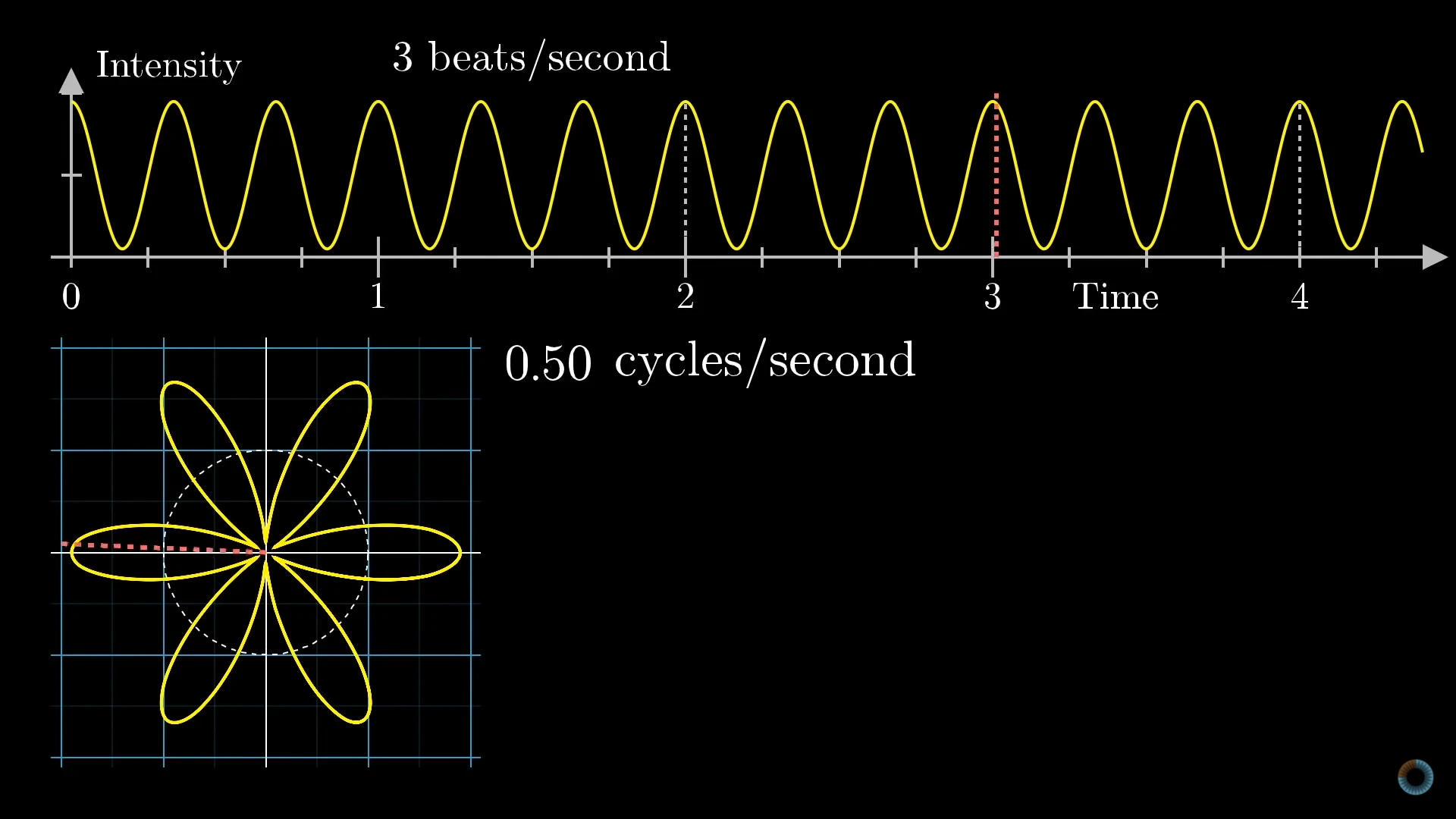
2 秒钟旋转 1 周

找到图像的质心，可以以质心距离原点的偏移量画出图像。可以发现一个有趣的结论：当旋转周期的倒数与频率一致时，质心距离原点的偏移最大。而当我们把两个波叠加在一起之后，质心偏移的图像也同样叠加在一起了。也就是说，画出叠加后的波的质心偏移图像和直接将质心偏移图相加的结果是一样的：

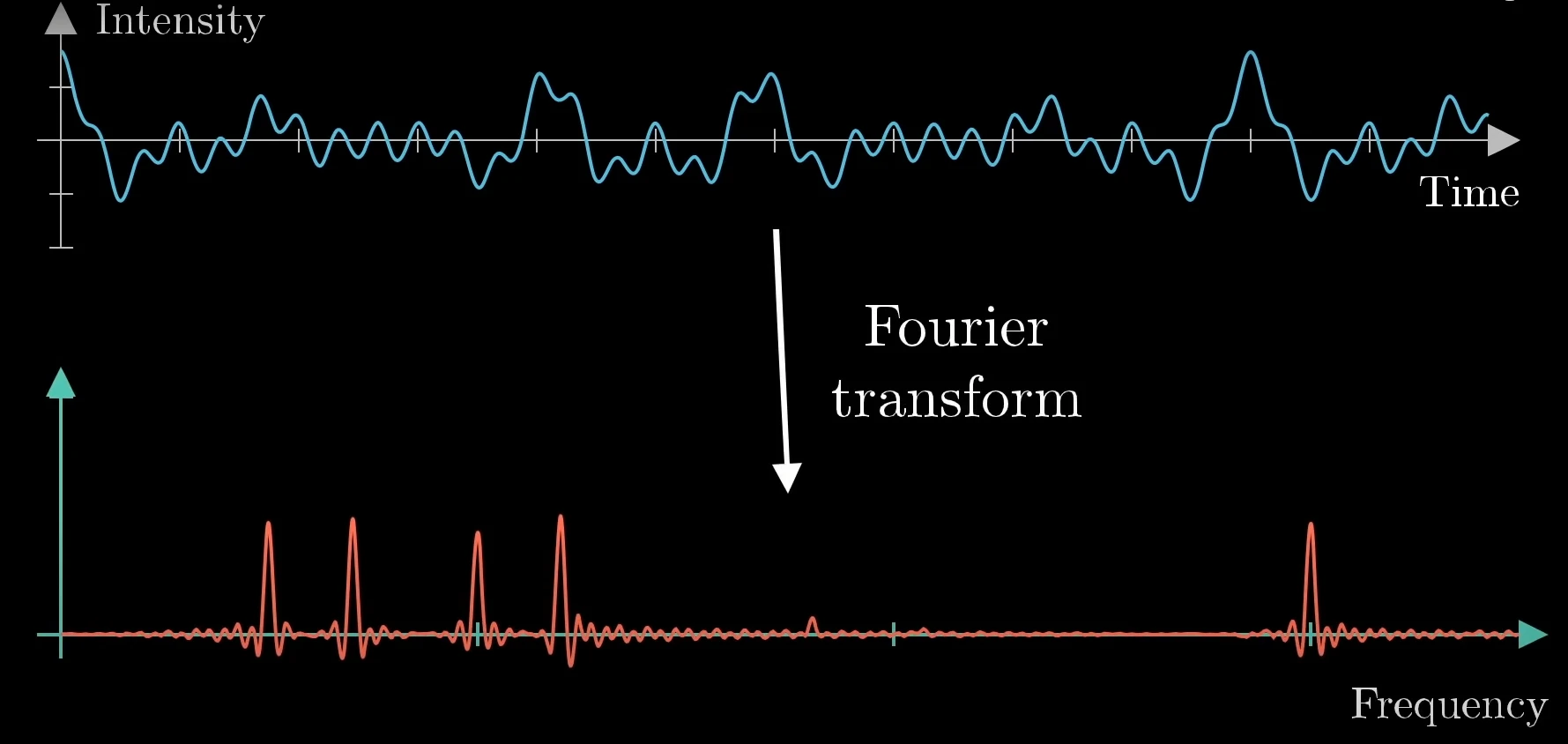
自然界中的许多东西都可以以信号的形式出现，最经典的例子就是声音，但声音信号往往是非周期性的。不过通过傅里叶变换公式，可以把非周期性的信号从时域转换到频域。下图显示了一段信号的转换，可见信号大多集中在低频段，高频段只有一个突出的波峰。
同样的，如果我们有信号的频域信息，可以通过逆傅里叶变换反过来得到时域信息。

逆傅里叶变换

通过变换，我们可以用滤波器对频域进行过滤，例如音频处理中经典的高通滤波和低通滤波。

公式解读

第一步：
$$\hat{g}(f)=\int_{-\infty}^{\infty}g(t)e^{-2\pi ift}dt$$
这个公式指的是时域信号 $g(t)$ 与 $e^{-2\pi ift}$ 相乘后对其在正无穷到负无穷的范围上求积分，$\hat{g}(f)$ 就是得到的频域。这个 $e^{-2\pi ift}$ 是什么？实际上，如果将 $f(t) = e^{-2\pi ift}$ 画在虚数坐标系（x轴表示实部，y轴表示虚部）上的话会是一个圆，$f$ 指频率，$2\pi$ 指周期，负号则让t递增时点是以逆时针的形式画在圆上的（控制方向）。下图是圆上的一些特殊点：

特殊点

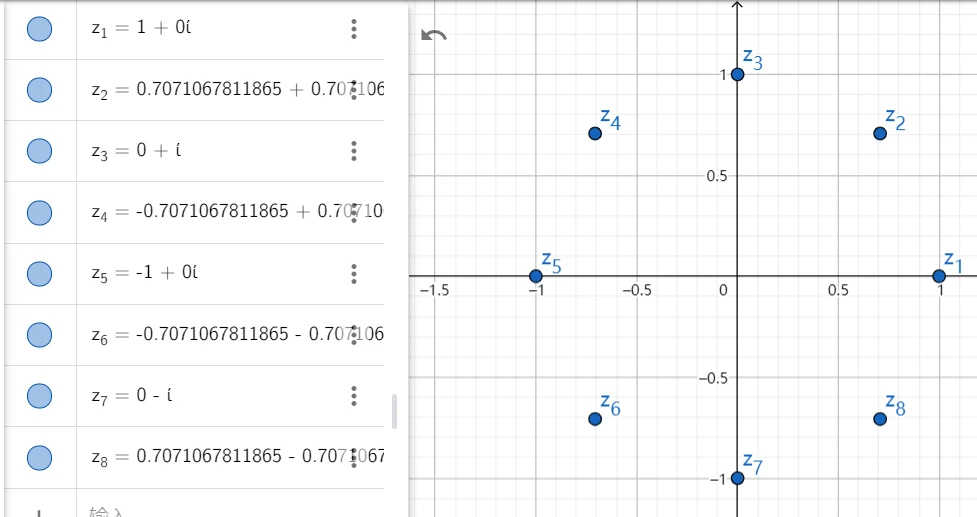
当 $g(t)$ 与 $e^{-2\pi ift}$ 相乘，我们得到了前文提到的曲线。随着截取频率 $f$ 的改变，相乘的结果 $\hat{g}(f)$ 也会随之改变，这和前文的变化是一样的。

随后，追踪曲线的重心坐标，就可以绘制出频域图。不过，有一些小小的修改。
$$\frac{1}{t_{2}-t{1}} \int_{t_{1}}^{t_{2}} g(t)e^{-2\pi ift}dt$$
$t_{2}$ 和 $t_{1}$指截取的两个时间点，上式的结果表示曲线的重心位置。然而真正的傅里叶变换公式舍弃了 $\frac{1}{t_{2}-t{1}}$ 的部分，表示质心坐标乘以该频率的持续时间。

但通常的，我们都是站在无穷的角度进行积分的，无穷包含了所有的时间段，即
$$\int_{-\infty}^{\infty} g(t)e^{-2\pi ift}dt$$

离散傅里叶变换

计算机中的信号往往用离散的数据表示，例如针对一个信号采样得到的点 $X_{0},X_{1},X_{2},…,X_{N}$ 。离散傅里叶变换其实是针对离散数据的傅里叶级数，和函数并没有关系：

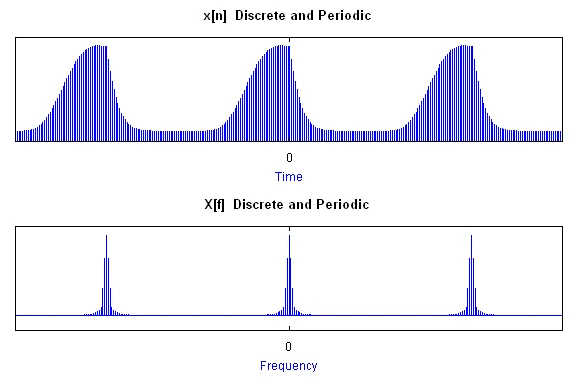
离散傅里叶变换

公式解读

离散傅里叶变换公式为：
$$\hat{f}{k} = \sum{j = 0}^{N - 1} f_{j}e^{kj\frac{-2\pi i}{n}}$$
$f_{j}$ 表示采样点 $X_{j}$ 对应的频率，相当于 $g(t_{j})$ 的值，$\hat{f}_{k}$ 表示截取频率为 $k$ 时的结果，表示为所有采样点计算结果的和。$n$ 表示采样点的总数， $e^{\frac{-2\pi i}{n}}$ 和前文的概念类似，除以 $n$ 使得在 $n > 1$ 时旋转一周的周期变大。

下图展示了有10个采样点时的情况。可以看到原本为 $2\pi$ 的 $\omega$ 变成了 $20\pi$

其实我们可以写作矩阵乘法的形式，因为计算的是分立的每一项 $\hat{f_{k}}$，输入的结果也是离散的数据 $f_{j}$。令 $e^{\frac{-2\pi i}{n}} = \omega_{n}$ ，代入 $k$ 为不同频率时的特殊值，寻找其中的规律，可以推出：
$$\begin{pmatrix}
\hat{f_{0}} \
\hat{f_{1}} \
\hat{f_{2}} \
\vdots \
\hat{f_{n}} \
\end{pmatrix} =
\begin{pmatrix}
1 & 1 & 1 & \cdots & 1 \
1 & \omega_{n} & \omega_{n}^{2} & \cdots & \omega_{n}^{n-1} \
1 & \omega_{n}^{2} & \omega_{n}^{4} & \cdots & \omega_{n}^{2(n-1)} \
1 & \vdots & \vdots & \vdots & \vdots \
1 & \omega_{n}^{n-1} & \omega_{n}^{2(n-1)} & \cdots & \omega_{n}^{(n-1)^{2}} \
\end{pmatrix}
\begin{pmatrix}
f_{0} \
f_{1} \
f_{2} \
\vdots \
f_{n} \
\end{pmatrix}
$$
其中，$\begin{pmatrix}1 & 1 & 1 & \cdots & 1 \1 & \omega_{n} & \omega_{n}^{2} & \cdots & \omega_{n}^{n-1} \1 & \omega_{n}^{2} & \omega_{n}^{4} & \cdots & \omega_{n}^{2(n-1)} \1 & \vdots & \vdots & \vdots & \vdots \1 & \omega_{n}^{n-1} & \omega_{n}^{2(n-1)} & \cdots & \omega_{n}^{(n-1)^{2}} \\end{pmatrix}$即为DFT矩阵，通常用 $F_{n}$表示，$n$ 为具体项数。计算的结果不单纯包含振幅 $A$ ，还包含了相位 $\varphi$。

DFT的逆变换公式为如下，从总和里拆分出了原本离散点的信息：
$$f_{k} = \frac{1}{n} \sum_{j = 0}^{N - 1} \hat{f}_{j}e^{-2\pi ij\frac{k}{n}}$$

快速傅里叶变换

FFT是20世纪最强大且优雅的算法。
FFT是DFT的一种计算方法，它可以快速处理更庞大的数据集，所以我们不用去构建前文提到的DFT矩阵。**DFT的时间复杂度达到了 $O(N^2)$，而FFT仅需要 $O(n log(n))$**。FFT被广泛应用于图像压缩、音频压缩、信号处理以及接下来要介绍的海水模拟等多种场景中。
FFT的基本思想是将$\begin{pmatrix}f_{0} \f_{1} \f_{2} \\vdots \f_{n} \\end{pmatrix}$拆分成奇数和偶数两部分，采用分治思想和蝶形算法相组合。
原始DFT公式为：
$$X[k] = \sum_{n=0}^{N-1}x[n]e^{-i\frac{2\pi kn}{N}}$$
即
$$X[k] = \sum_{n=0}^{N-1}x[n]W^{k}{N}$$
拆出奇数部分 $H[x]$ 和偶数部分 $G[x]$，有：
$$X[k] = \sum{n=0}^{N-1}x[2n]W^{k}{\frac{N}{2}} + W{N}^{k}\sum_{n=0}^{N-1}x[2n+1]W^{k}{\frac{N}{2}}, k\in(0,1,…,\frac{N}{2}-1)$$
最后推导得出下式（推导过程可以参考参考资料中的fft海面模拟(二)）
$$X[k] = G[k] + W{N}^{k}H[k], k\in(0,1,…,\frac{N}{2}-1)$$
$$X[k] = G[k-\frac{N}{2}] + W_{N}^{k}H[k-\frac{N}{2}], k\in(\frac{N}{2},\frac{N}{2} + 1,…,N-1)$$
假设N = 8，根据推导的结果，可以画出下图所示的关系网图：

现在得到了N –> N/2的图，还可以继续划分下去，直到每个分组只剩一个元素位置。取一个特殊点吧，假设k = 0，则直接展开$X[k] = G[k] + W_{N}^{k}H[k]$科研得到：
$$X[0] = x[0]W_{4}^{0} + x[2]W_{4}^{0} + x[4]W_{4}^{0} + x[6]W_{4}^{0} + W_{8}^{0}(x[1]W_{4}^{0} + x[3]W_{4}^{0} + x[5]W_{4}^{0} + x[7]W_{4}^{0})$$
第二次进行拆分（拆开偶数 $G(x)$ 和奇数 $H(x)$，现在这两个部分各有4个元素，还可以两两拆开成新的奇偶对）：
$$X[0] = \textcolor{CornflowerBlue}{x[0]W_{2}^{0} + x[4]W_{2}^{0}} + W_{4}^{0}(\textcolor{LimeGreen}{x[2]W_{2}^{0} + x[6]W_{2}^{0}}) + W_{8}^{0}(\textcolor{CornflowerBlue}{x[1]W_{2}^{0} + x[5]W_{2}^{0}} + W_{4}^{0}(\textcolor{LimeGreen}{x[3]W_{2}^{0} + x[7]W_{2}^{0}}))$$

通过推算，可以得到k为不同数时的结果，并可以根据结果画出蝶形网络。蝶形网络在N相同时表现的形式是一样的：

不过，在后续实际操作时使用到的是IDFT，所以说实际上是要倒过来求的…
IDFT的公式为：
$$f_{k} = \frac{1}{n} \sum_{j = 0}^{N - 1} \hat{f}_{j}e^{-2\pi ij\frac{k}{n}}$$
类似于先前FFT的推导模式，应用于IFFT，可以推导出IFFT的蝶形网络如下所示：

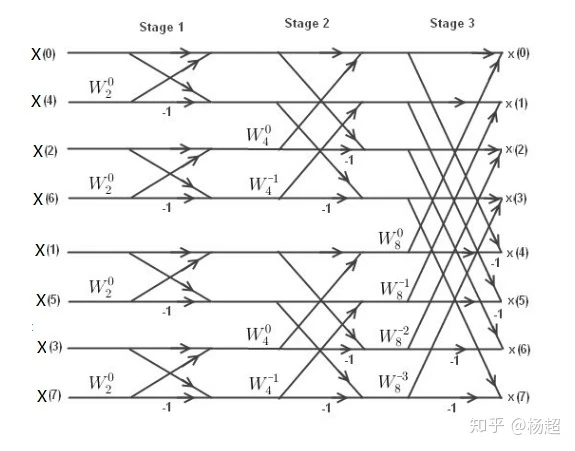
IFFT的蝶形网络

现在，可以利用IFFT进行后续的海面模拟了。

从傅里叶变换到海面模拟

海面天然可以近似看作由数个不同的正弦波叠加的结果，这正好与从频域到时域的逆傅里叶变换结果相似（当我们知道频域信息之后，就可以逆推求时域信息，也就是充满很丰满叠加过波形了）。
那么该选取什么样的频谱比较好呢？在海洋频谱维基里我查到了三种频谱：

Phillips spectrum / 菲利普频谱
Pierson-Moskowitz Spectrum / P-M频谱
JONSWAP Spectrum / JONSWAP频谱

首次提出FFT模拟海浪的Simulating Ocean Water一文中使用菲利普频谱进行模拟，同时我查到的一篇2019年的博客也使用同样的菲利普频谱+FFT的方法模拟海浪，证明该方法在FFT模拟领域的经久不衰。不过我们还可以使用JONSWAP频谱 + 泊松分布的形式进行模拟。
到这一步觉得已经差不多了？没有，后面还有很多计算（

歪日啊沃土辣

先看看海面IDFT的公式吧：
$$h(\vec{x}, t) = \sum_{\tilde{k}}\tilde{h}(\tilde{k},t)e^{i\vec{k}\vec{x}}$$
这是一个二维的逆傅里叶变换，并且结果随着时间改变（动态海浪）。$\vec{x}$ 指时域坐标 $(x,z)$，$\vec{k}$ 指频域坐标 $(k_x,k_z)$，$\tilde{h}(\tilde{k},t)$ 指频域中的海洋高度场函数。

$k_x = \frac{2\pi n}{L_x}$，$k_z = \frac{2\pi m}{L_z}$，$m$ 和 $n$ 的范围都在 $-\frac{N}{2}$ 到 $\frac{N}{2}-1$ 之间，$L_x$、$L_z$ 指海面x或z方向的大小。为了后续计算更加简便，可以令 $L_x$ 和 $L_z$ 大小相等
$x = \frac{u L_x}{N}$，$z = \frac{v L_z}{N}$，$u$ 和 $v$ 的范围都在 $-\frac{N}{2}$ 到 $\frac{N}{2}-1$ 之间
时域和频域都有 $N*N$ 个点。通常，$N$ 取到64足够呈现超棒的效果
标量形式：$h(x, z, t) = \sum_{m=-\frac{N}{2}}^{\frac{N}{2}-1} \sum_{n=-\frac{N}{2}}^{\frac{N}{2}-1}\tilde{h}(k_x,k_z,t)e^{i(k_x x+k_z z)}$，带入 $k_x$ 和 $k_z$ ，则有
$$h(x, z, t) = \sum_{m=-\frac{N}{2}}^{\frac{N}{2}-1} \sum_{n=-\frac{N}{2}}^{\frac{N}{2}-1}\tilde{h}(\frac{2\pi n}{L_x},\frac{2\pi m}{L_z},t)e^{i(\frac{2\pi n}{L_x} x+\frac{2\pi m}{L_z} z)}$$
为使求和下标从0开始，使用 $m’ = m+\frac{N}{2}$ 和$n’ = n+\frac{N}{2}$ 替换，则有
$$h(x, z, t) = \sum_{m’=0}^{N-1} \sum_{n’=0}^{N-1}\tilde{h}(\frac{2\pi (n’-\frac{N}{2})}{L_x},\frac{2\pi (m’-\frac{N}{2})}{L_z},t)e^{i(\frac{2\pi (n’-\frac{N}{2})}{L_x} x+\frac{2\pi (m’-\frac{N}{2})}{L_z} z)}$$
化简一下，令 $\tilde{h}’ (n’,m’,t) = \tilde{h}(\frac{2\pi (n’-\frac{N}{2})}{L_x},\frac{2\pi (m’-\frac{N}{2})}{L_z},t)$，并从 $e^{i(\frac{2\pi (n’-\frac{N}{2})}{L_x} x+\frac{2\pi (m’-\frac{N}{2})}{L_z} z)}$ 中提取出 $e^{i(\frac{2\pi (m’-\frac{N}{2})}{L_z} z)}$，得到
$$h(x, z, t) = \sum_{m’=0}^{N-1} e^{i(\frac{2\pi (m’-\frac{N}{2})}{L_z} z)} \sum_{n’=0}^{N-1}\tilde{h}(n’,m’,t)e^{i(\frac{2\pi (n’-\frac{N}{2})}{L_x} x)}$$
令 $\tilde{h}’’(x,m’,t) = \sum_{n’=0}^{N-1}\tilde{h}’(n’,m’,t)e^{i(\frac{2\pi (n’-\frac{N}{2})}{L_x} x)}$，则
$$h(x, z, t) = \sum_{m’=0}^{N-1} \tilde{h}’’(x,m’,t)e^{i(\frac{2\pi (m’-\frac{N}{2})}{L_z} z)}$$
由于L长度可随意选取，为向IDFT形式靠拢，取 $L = N$，得：
$$\tilde{h}’’(x,m’,t) = (-1)^{x}\sum_{n’=0}^{N-1}\tilde{h}’(n’,m’,t)e^{i\frac{2\pi n’ x}{N}}$$
$$h(x, z, t) = (-1)^{z}\sum_{m’=0}^{N-1} \tilde{h}’’(x,m’,t)e^{i\frac{2\pi m’z}{N}}$$
前文说到$x = \frac{u L_x}{N}$，$z = \frac{v L_z}{N}$，类似的，为了使下标从0开始，用$u’ = u + \frac{N}{2}$ 取代 $u$，则有：
$$\tilde{h}’’(u’-\frac{N}{2},m’,t) = (-1)^{u’-\frac{N}{2}}\sum_{n’=0}^{N-1}\tilde{h}’(n’,m’,t)e^{i\frac{2\pi n’ u’}{N}}(-1)^{n’}$$
$$h(u’-\frac{N}{2}, v’-\frac{N}{2}, t) = (-1)^{v’-\frac{N}{2}}\sum_{m’=0}^{N-1} \tilde{h}’’(u’-\frac{N}{2},m’,t)e^{i\frac{2\pi m’v’}{N}}(-1)^{m’}$$
为了能套入IFFT中计算，这个形式还不够。令：
$$A(u’,v’,t) = \frac{h(u’-\frac{N}{2}, v’-\frac{N}{2}, t)}{(-1)^{v’-\frac{N}{2}}}$$
$$B(u’,m’,t) = \tilde{h}’’(u’-\frac{N}{2},m’,t)(-1)^{m’}$$
$$C(u’,m’,t) = \frac{\tilde{h}’’(u’-\frac{N}{2},m’,t)}{(-1)^{u’-\frac{N}{2}}}$$
$$D(n’,m’,t) = \tilde{h}’(n’,m’,t)(-1)^{n’}$$
则有：
$$A(u’,v’,t) = \sum_{m’=0}^{N-1}B(u’,m’,t)e^{i\frac{2\pi m’v’}{N}}$$
$$C(u’,m’,t) = \sum_{n’=0}^{N-1}D(n’,m’,t)e^{i\frac{2\pi n’ u’}{N}}$$
现在这个形式符合 $T_{N}^{x}=e^{\frac{i2\pi x}{N}}$，可以套用IFFT了

Phillips-Gaussian频谱

Phillips-Normal频谱的含义为菲利普频谱 + 高斯分布的数据。Simulating Ocean Water一文中使用菲利普频谱进行模拟，同时我查到的大多数FFT海浪模拟的博客也使用同样的方法模拟海浪。菲利普频谱的公式为：
$$\tilde{h}(\vec{k},t) = \tilde{h}{0}(\vec{k})e^{i\omega (k)t} + \tilde{h}{0}^{*}(-\vec{k})e^{-i\omega (k)t}$$
先了解几个基本关系，下面的结论来自海洋统计学模型，可以在参考资料中找到海洋频谱相关的内容。

$\tilde{h}{0}$ 是时间 $t=0$ 时初始值的表达，$\tilde{h}{0}^{*}$ 表示 $\tilde{h}_{0}$的共轭复数（两个实部相等，虚部互为相反数的复数）
$k$ 表示 $\vec{k}$ 的模长，$k$ 本身的意思是波长
$\omega (k) = \sqrt{gk}$ 表示频率，其中 $g$ 为重力加速度
$\tilde{h}{0}(\vec{k}) = \frac{\xi{r} + i\xi_{i}}{\sqrt{2}}\sqrt{P_{h}(\vec{k})}$ ,其中 $\xi_{r}$ 和 $\xi_{i}$ 是相互独立的随机数，均服从均值为0，标准差为1的高斯分布
$P_h(k) = A\frac{e^{\frac{-1}{(kL)^2}}}{k^4}\vert \vec{k}\cdot\vec{w}\vert ^2$，$A$ 是一个数字常量，$w$ 表示风向
$L = \frac{v^2}{g}$

代回海面IDFT

在海面IDFT的介绍部分，为了使求和下标从0开始，我们把 $n$ 和 $m$进行了替换，并使用下式对替换后的式子进行化简：
$$\tilde{h}’ (n’,m’,t) = \tilde{h}(\frac{2\pi (n’-\frac{N}{2})}{L_x},\frac{2\pi (m’-\frac{N}{2})}{L_z},t)$$
将其代入菲利普频谱$\tilde{h}(\vec{k},t) = \tilde{h}{0}(\vec{k})e^{i\omega (k)t} + \tilde{h}{0}^{}(-\vec{k})e^{-i\omega (k)t}$中，可得：
$$\tilde{h}(n’,m’,t) = \tilde{h}{0}(n’,m’)e^{i\omega ‘ (n’,m’)t} + \tilde{h}{0}^{}(-n’,-m’)e^{-i\omega ‘(n’,m’)t}$$
由 $\omega (k) = \sqrt{gk}$ 可得 $\omega ‘ (n’,m’)$计算为：
$$\omega ‘(n’,m’) = \sqrt{g\sqrt{(\frac{2\pi n’-\pi N}{L_x})^{2} + (\frac{2\pi m’-\pi N}{L_z})^{2}}}$$
由 $\tilde{h}{0}(\vec{k}) = \frac{\xi{r} + i\xi_{i}}{\sqrt{2}}\sqrt{P_{h}(\vec{k})}$ 可得：
$$\tilde{h}’{0}(n’,m’) = \frac{\xi{r} + i\xi_{i}}{\sqrt{2}}\sqrt{P_{h}(n’,m’)}$$
由 $P_h(k) = A\frac{e^{\frac{-1}{(kL)^2}}}{k^4}\vert \vec{k}\cdot\vec{w}\vert ^2$可得：
$$P’h(n’,m’) = A\frac{e^{\frac{-1}{(\sqrt{n’^2 + m’^2}L)^2}}}{k^4}\vert (n’,m’)\cdot\vec{w}\vert ^2$$
并且 $n’$ 和 $m’$ 的值已知，为：$n’=\frac{2\pi (n’-\frac{N}{2})}{L_x}$，$m’=\frac{2\pi (m’-\frac{N}{2})}{L_z}$
$\tilde{h}{0}^{*}$可以通过.conj()函数求 $\tilde{h}_{0}$ 的共轭，其余推导部分和前文一样，就不再写一遍了。
写到这里你可能已经不知道现在得到的 $\tilde{h}’(n’,m’,t)$ 要怎么用了，总结一下海面IDFT+菲利普频谱的流程：

计算 $\tilde{h}’(n’,m’,t)$
计算 $D(n’,m’,t) = \tilde{h}’(n’,m’,t)(-1)^{n’}$
根据 $C(u’,m’,t) = \sum_{n’=0}^{N-1}D(n’,m’,t)e^{i\frac{2\pi n’ u’}{N}}$ ，对其进行IFFT操作计算 $C(u’,m’,t)$
根据 $B(u’,m’,t) = C(u’,m’,t)(-1)^{m’+u’-\frac{N}{2}}$ 计算 $B(u’,m’,t)$
根据 $A(u’,v’,t) = \sum_{m’=0}^{N-1}B(u’,m’,t)e^{i\frac{2\pi m’v’}{N}}$ ，对其进行IFFT操作计算 $A(u’,v’,t)$
根据 $h(x,z,t) = A(u’,v’,t)(-1)^{v’-\frac{N}{2}}$ 计算 $h(x,z,t)$

基本思路有了，在Unity中怎么实现呢？前两篇水体模拟我都用了shader graph直接写顶点变换，FFT由于涉及大量复数计算，shader graph并不支持。下篇文章将采用传统shaderLab + computed shader + csharp方式计算。
（不知道能不能写出来（大概还得一周吧，慢慢来