介绍

Sin Wave的局限

在引入Gerstner Wave之前，人们更多使用正弦波来模拟海浪，因为正弦波天生具有类似海浪的形状。但它的局限也很明显，那就是波峰过于圆润，纵然有办法通过代数方法约束波峰的形状，但效果还是无法达到预期的尖锐。

瞧这圆滚滚的波峰

什么是Gerstner Wave

Gerstner Wave是Sin Wave的后继者，到现在也是一种常用的用来模拟海洋波浪的算法。他的历史其实已经很古老了，可以追溯到1986年。相比于快速傅里叶变换(FFT)，Gerstner Wave方法的开销更小，效果也很真实，因此被更多的应用与游戏领域（FFT更适合影视行业，因为它的效果更好但开销更大）。
Gerstner Wave的公式如下：
$$P(x,y,t) = \begin{pmatrix}x + \sum({Q_{i}A_{i} * D_{i}.x * \cos(\omega_{i} D_{i}(x,y) + \varphi t})) \y + \sum({Q_{i}A_{i} * D_{i}.y * \cos(\omega_{i} D_{i}(x,y) + \varphi t})) \\sum({A_{i} * \sin(\omega_{i} D_{i}(x,y) + \varphi t})) \end{pmatrix}$$

其中x和y表示任一顶点的水平面坐标（在unity中对应x和z），t表示时间。前两行代表顶点在xy平面做cos变化，第三行表示顶点的高度轴（在unity中为y）做sin变化。如果可视化Gerstner Wave中每一个顶点的运动情况，则有下图的结果：

这代表顶点在做圆周运动，这是因为x方向为 $cos$ 函数，高度方向为 $sin$ 函数的原因。$sin^2 + cos^2 = 1$

在Unity中实现

由上公式，我们可以剥离出几个控制变量：

$Height$，即$A_{i}$，表示浪的高度
$Speed$，即$\varphi_{i}$，因为与时间相乘，表示浪的运行速度
$T$，即周期，用来在后续表示$\omega$
$Sharp$，即尖锐程度$Q_{i}$，控制浪尖的尖锐程度
$WaveDir$，即浪的运动方向(Wave Direction)

为了避免float类型的变量太多导致材质参数过多，这回我把Height\Speed\T\Sharp封装到了一个vec4变量中

用到了group一组节点的功能，可以起到注释的作用

其余渲染的部分可以参照上一篇文章(水体渲染)，这里用模型高度插值加了一个浪尖白沫，其他是一样的。

步骤

利用已有变量计算 $\omega$ 和 $Q_{i}$
$\omega = \frac{2\pi}{T}$ 就不用多说了，$Q_{i} = \frac{Sharp}{\omega * A}$。$Q_{i}$ 是控制波浪陡度的参数，$Q_{i}$ 为0表示通常的滚动正弦波，$Q_{i} = \frac{1}{\omega * A}$表示尖峰，加入sharp控制尖锐程度
计算x、z和y的部分，组装乘vec3后与Position相加
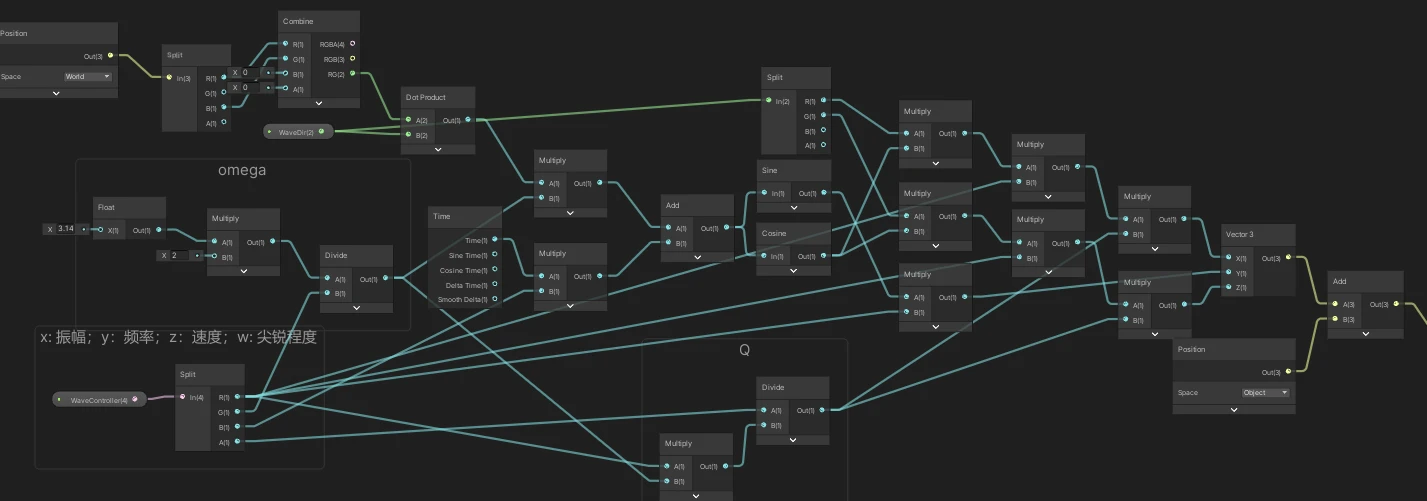
Gerstner Wave的公式已经给出，现在也计算好了 $\omega$ 和 $Q_{i}$，所以直接组合公式即可。计算完成后将x、y、z的结果组装成Vec3，与Position节点相加后输出