为什么会写这篇文章呢…因为我已经在大大小小的场合中遇到三次相关的题目了，前几次答得挺不尽人意的。第一次是在剑心互娱的校招笔试上，要求画一个黑灰白三条杠（下左），第二次是字节的二面要求画一个棋盘格的效果（下右），还有一次忘了（

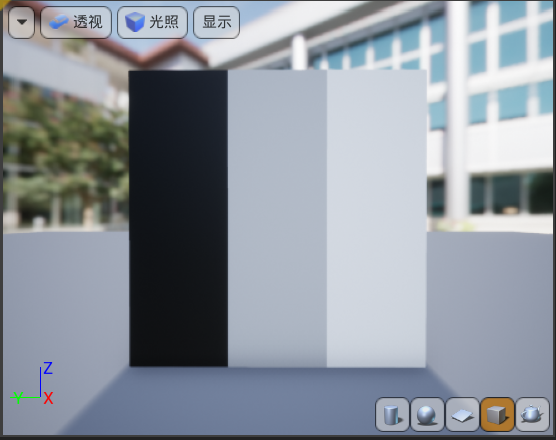
对于这两种效果，我们的思路其实是一样的（棋盘格只需要多一步加法）。

开始绘制

怎么用程序画东西呢？我们在做材质的时候似乎一直是基于贴图进行处理的。实际上，我们是可以直接对纹理映射（texcoord节点）下手的，如果将其连接到根节点的base color，我们会得到如下画面：

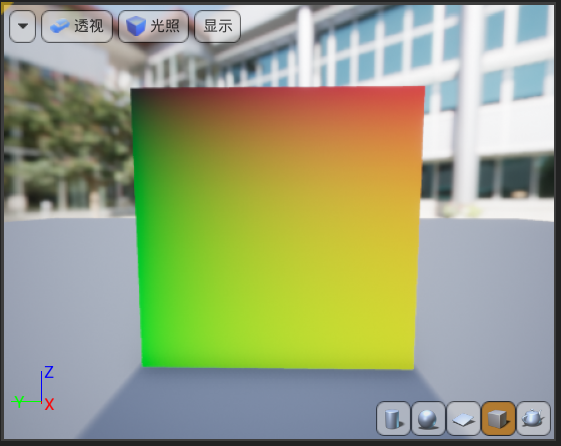
为什么是这个颜色？首先需要知道的是：texcoord只有uv两个量，而颜色具有三个分量。当我们默认第三个分量为0时，就会得到上述的颜色信息。而如果我们把第三个分量设置为1，就会得到：

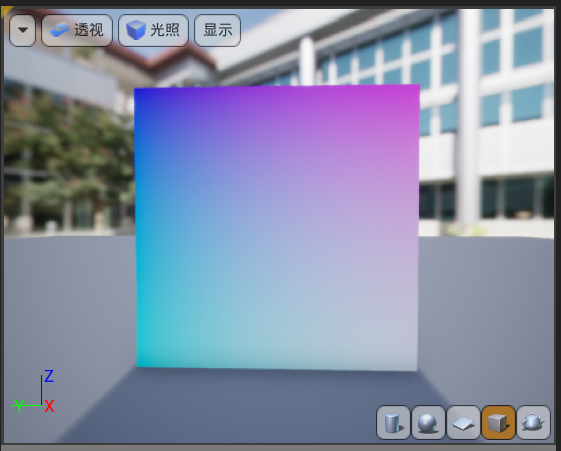
数学处理

为了实现三条边、四条边甚至多边的情况，我们需要对texcoord进行缩放，这一步很简单，只需要让texcoord乘上一个用来控制的常量：

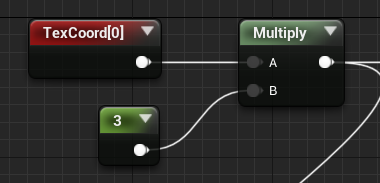
然后，对texcoord的值进行取整（floor节点）。这一步的目的是将贴图“阶梯化”，方便后续实现黑白分条的效果。下图好像并没有出现理想的分条效果，因为黄色的部分的uv值已经超过1了，程序自动用1填补了原本的值：

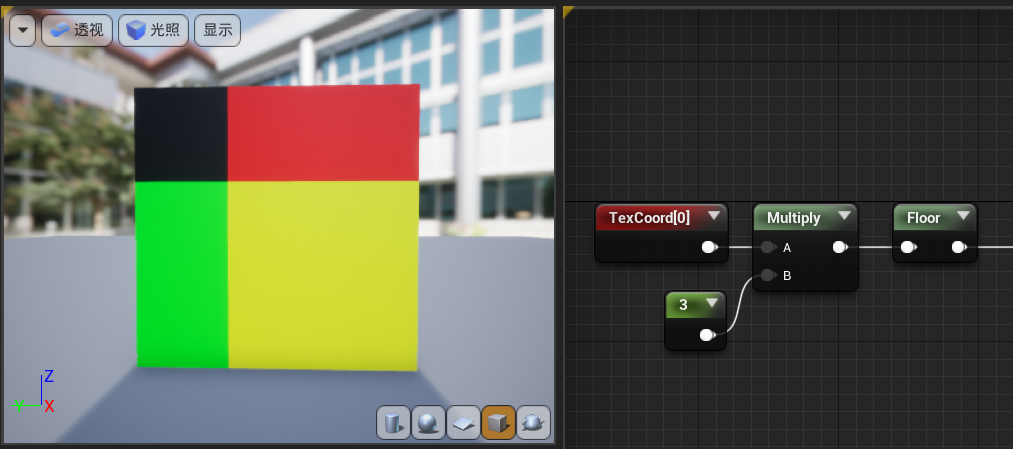
接下来我们对uv坐标除以2，这样坐标对应的值就变成了0，0.5，1，1.5，2，…，灰色开始出现

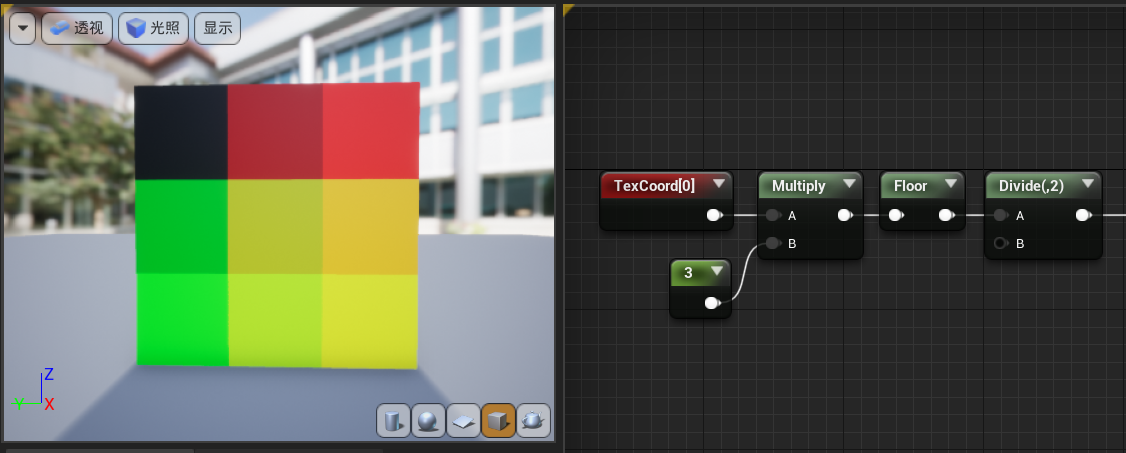
接下来，我们把u和v从这张红红绿绿的图里解码出来，单独输出R通道（u）的结果如下所示：

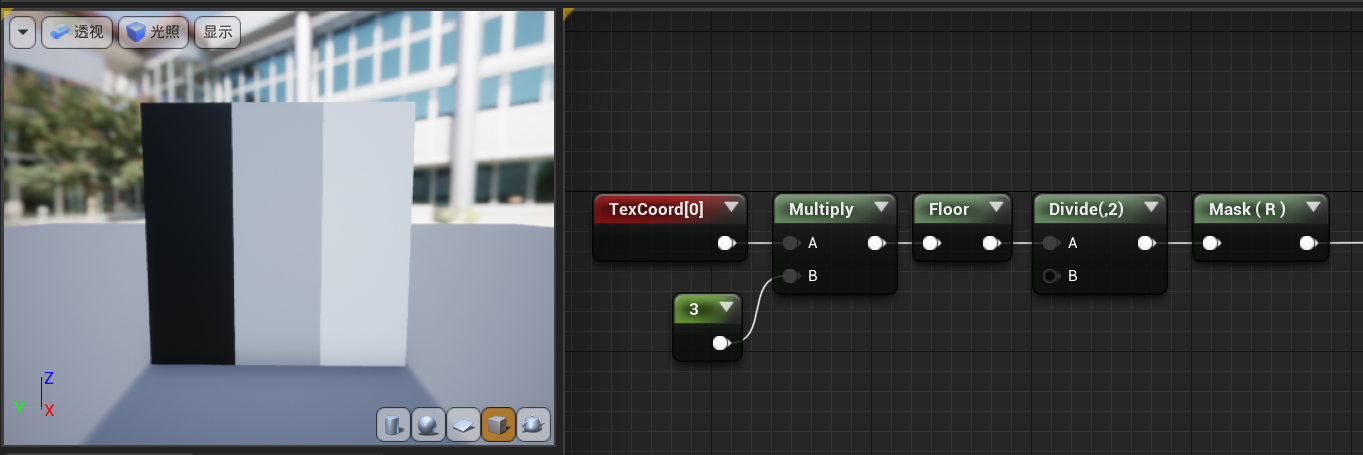
这就是我们要的黑灰白三条杠的效果了。

我们将在三条杠的基础上实现棋盘效果。把R通道的信息和G通道相加：

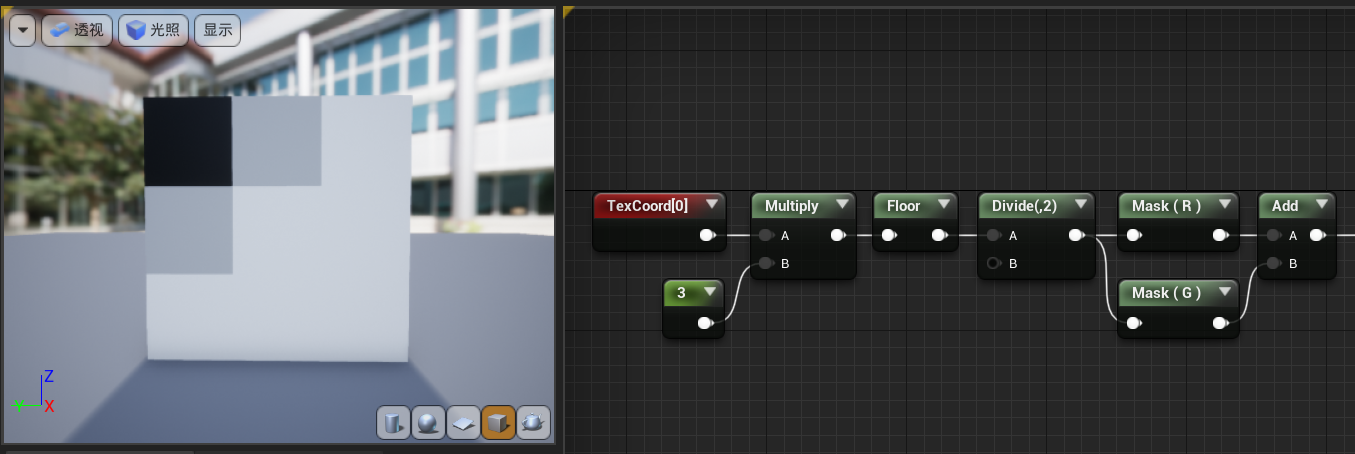
结果很不尽人意，因为超出的部分都变成了1（也就是白色的块），盘上还有灰色的块。现在我们需要的是一个黑白的棋盘，也就是说我们的颜色只能有0和1。
怎么实现黑白的效果呢？现在其实我们的数学结果其实是这样的：

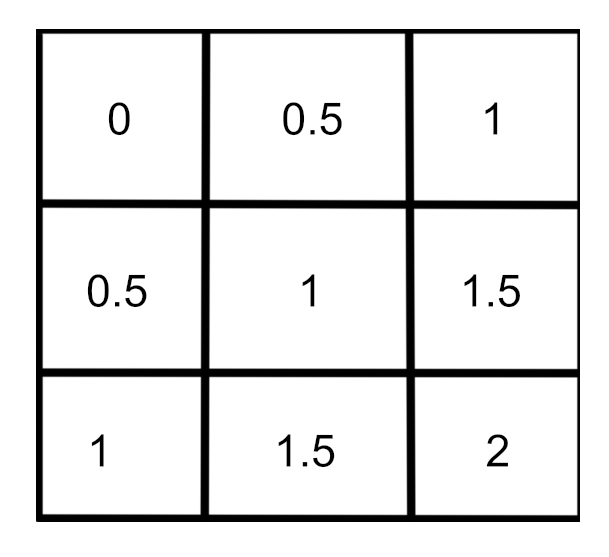
如果只保留小数点部分，我们就可以得到比较合适的图了，只不过现在看上去是白色的部分其实是值为0.5的灰色。

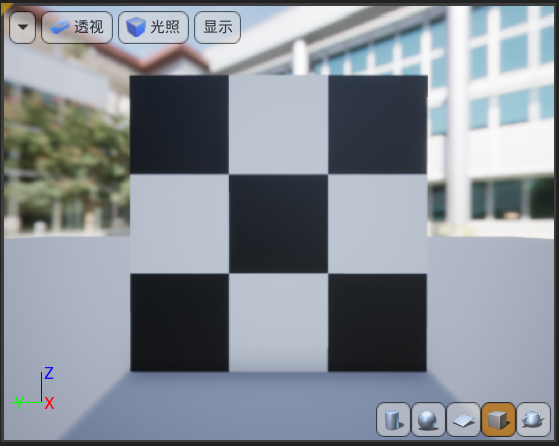
我们还需要进行最后一步，也就是*2的操作才能得到真正的黑白棋盘。对比上图的“黑灰棋盘”还是有点区别的。
（其实我一开始写的时候忘记乘2了，因为这个灰色比较淡，又在黑色边上，一下子没看出来）

实际场景应用效果：